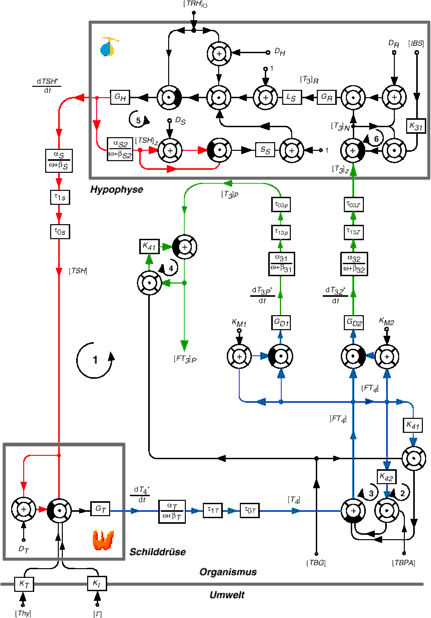
Thyrotropic Feedback Control   Mathematical models of the pituitary-thyroid axis: In 1940, eleven years after the discovery of the thyrotropic hormone TSH by Aron in the year 1929, W. T. Salter postulated the existence of a control loop linking the pituitary and thyroid gland. This idea was inspired by the recent description of the two gonadotropic feedback control loops. Only a few years later, Astwood and Hoskins could reveal both the existence and the pathophysological relevance of this thyrotropic feedback control system. In 1968, Panda and Turner succeeded in a quantitative description ot the interdependence of thyroxine and TSH levels, but the first mathematical models of the feedback loop had already been developed up to 12 years earlier. Over the years, these models were increasingly improved. As a consequence of this continued evolution, some of the newest models [Dietrich 2001, Dietrich et al. 2004 and Eisenberg et al. 2010] are also suitable for medical decision making. Today, modelling of thyrotropic feedback control is faced with the challenge of newly discovered complexities in the information processing structure, e. g. Ultrashort feedback control of TSH secretion (Kakita-Laborde-Odell loop and Brokken-Wiersinga-Prummel loop) and long-feedback of iodothyronines on hypothalamic TRH release (Fekete-Lechan loop). For a more comprehensive review of mathematical models of thyroid homeostasis see Dietrich et al. 2012. A selection of historic and modern models: Model Year Transfer characteristics Information processing structure Danziger and Elmergreen   1956   linear phenomenological Roston 1959 linear with basal secretion phenomenological Norwich and Reiter 1965 linear phenomenological DiStefano and Stear 1968 linear with basal secretion phenomenological, partly parametrically isomorphic DiStefano 1969 linear with basal secretion phenomenological, partly parametrically isomorphic DiStefano et al. 1975 N/A parametrically isomorphic Saratchandran et al. 1976 logarithmic / linear phenomenological, partly parametrically isomorphic Seif 1977 logarithmic / linear phenomenological, partly parametrically isomorphic Wilkin 1977 limit elements phenomenological, partly parametrically isomorphic Cohen 1990 exponential phenomenological Li et al. 1995 complex polynoms phenomenological, partly parametrically isomorphic Dietrich et al. 1997 Michealis-Menten kinetics and linear elements partly parametrically isomorphic (Model 2 - see below) Dietrich et al. 1997 MiMe-NoCoDi model parametrically isomorphic (Model 7.1 - see below ) Dietrich et al. 1998 MiMe-NoCoDi model parametrically isomorphic (Model 9 - see below ) Dietrich et al. 2001 MiMe-NoCoDi model parametrically isomorphic (Model 10 - see below ) Degon et al. 2005 based on compartment and flux analysis   parametrically isomorphic, but intrathyroidal kinetics only Leow 2007 Second order Bernoulli differential equations with hysteresis, inverse exponental power law of TSH response partly parametrically isomorphic Eisenberg et al. 2010 Based on DiStefanos models from 1968, 1969 and 1975 parametrically isomorphic   Versions of nonlinear models based on or related to the MiMe-NoCoDI model: Version Comment 1 Michaelis-Menten kinetics in pituitary and thyroid gland (II-1997) 2 Introduction of time constants, plasma protein binding also for T3 (II-1997, presented at ETA '97) 3 Michaelis-Menten kinetics for 5'-Dejodinase 4 Type I and Type II 5'-Dejodinase differentiated 5 Feedback term changed (abandoned again, VIII-1997) 6 Feedback term corrected (VIII-1997) 7 Non competitive quotient inhibition in form of v-type allostery, plasma protein binding for T3 addressed in a more differentiated manner (VIII-1997) 7.1 Changed name conventions (XI-1997, presented in the colloqium of endocrine methods, university of Munich) 8 Ultra-short feedback in anterior pituitary introduced (IV-1998) 9 Ultra-short feedback now covering Michaelis-Menten kinetics (V-1998, presented at Symposium Gentianum 1999) 9.1 Changed name conventions, disturbances better addressed in simulation (IV-1999) 10 Intracellular binding substrate introduced (presented at EMCSR 2002, published with Logos-Verlag and in CBS) 11 Introduction of Long-feedback at TRH site (planned)

tfc.medical-cybernetics.de

© 1995-2012 J. W. Dietrich | Imprint and Legal Information | Last Change: Mon, Dec 31, 2012